1. Числовые ряды
Числовой ряд

Этот ряд сходится, если существует предел
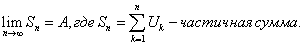
Необходимое условие сходимости ряда
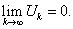
Признак Даламбера
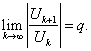
При q<1 ряд сходится; при q>1 ряд расходится; при q=1 вопрос о сходимости ряда остается открытым, т.е. ряд может как сходиться, так и расходиться.
Интегральный признак Коши
Пусть f(x) - такая функция, что f(k)=Uk (k=1, 2, ...). Тогда ряд ∑k=1∞Uk с положительными членами сходится, если существует несобственный интеграл ∫1∞f(x)dx, и расходится в противном случае.
Признак сходимости знакочередуещегося ряда
Знакочередующийся ряд U1-U2+U3-U4+...=∑k=1∞(-1)k+1Uk сходится, если limk→∞(Uk)=0 и Uk>Uk+1 (k=1,2,...)
Абсолютная и условная сходимости
Ряд с произвольными членами ∑k=1∞Uk сходится абсолютно, если сходится ряд ∑k=1∞|Uk|.
Если ряд ∑k=1∞Uk сходится, а ряд ∑k=1∞|Uk| расходятся, то первый ряд называется условно сходящимся.
Операции над абсолютно сходящимися рядами
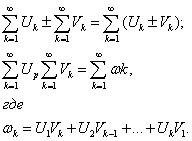
|
2. Функциональные ряды
Функциональный ряд
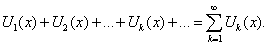
Этот ряд сходится при x=a, если сходится числовой ряд ∑k=1∞Uk(a)
Область сходимости функционального ряда - это множество тех значений x, при которых ряд сходится.
3. Степенные ряды
Областью сходимости степенного ряда
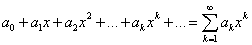
является промежуток (-R, R), где R - радиус сходимости.

Интегрирование и дифференцирование степенных рядов

Радиус сходимости этих рядов, полученных почленным дифференцированием и интегрированием, остается без изменений.
Ряд Тейлора
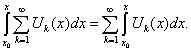
Ряд Маклорена

|